Job preferences

Utku Olcar

is open to work

Job titles

Robotics Engineer · Robotics Software Engineer · Robotics Specialist · Mechatronics Engineer · Embedded Software Engineer

Start date

Immediately, I’m actively applying

Job types

Full-time (I can work remotely)

If you are hiring, leave an email address, please.
Utku Olcar Logo

BUG Algorithm Application Using ROS (Robotik Operating System)




Details

I am going to explain my work about programming a navigation code inspired by the Bug0 Algorithm for the Turtlebot3 robot in the GAZEBO Simulation platform. I have programmed this algorithm in Robotic Operating System using Python programming language.

Robust control algorithms were not used in this work. This algorithm is programmed with position control only. The main idea is to use ROS development tools and systems like Action Server, Launch Files, rViz Visualization, TF Transformations, Gazebo Simulation, etc.

Youtube Link : Youtube Link

If you want to get the source code, please contact me.

What is the Bug0 Algorithm?

The Bug0 Algorithm is an autonomous navigation algorithm that uses only the sensor's data without any map. The algorithm has basically two different behaviors;

  • Behaviour 1: Head to goal straight
  • Behaviour 2: Follow the obstacle boundary

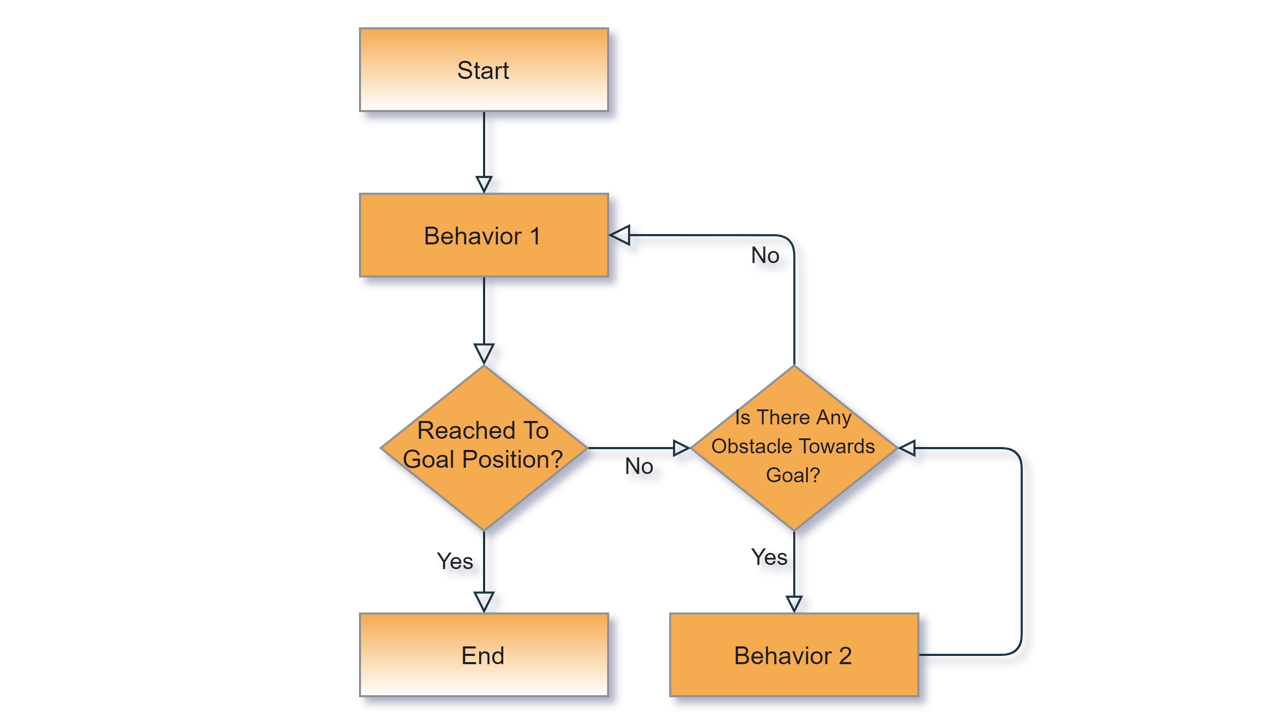
Bug0 Algorithm

The algorithm tells that the robot implements the "Behavior 1" and goes towards the goal position until an obstacle detected in front. If there is an obstacle, the robot changes behavior to "Behavior 2" and follows the obstacle boundary. When there is no obstacle between the robot and the obstacle, the robot executes the "Behavior 1" again. So, this loop continues until the robot reaches the goal position.

Behavior 1 (Head to Goal)

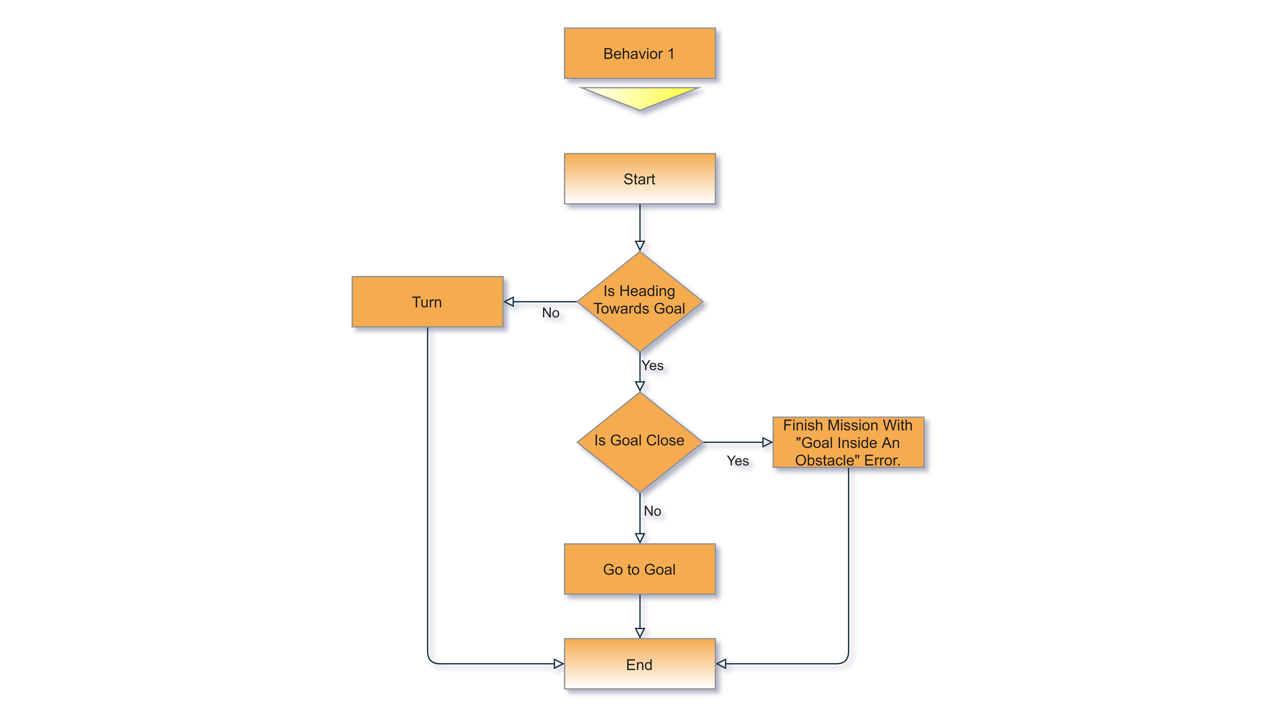
Bug0 Algorithm Behavior 1

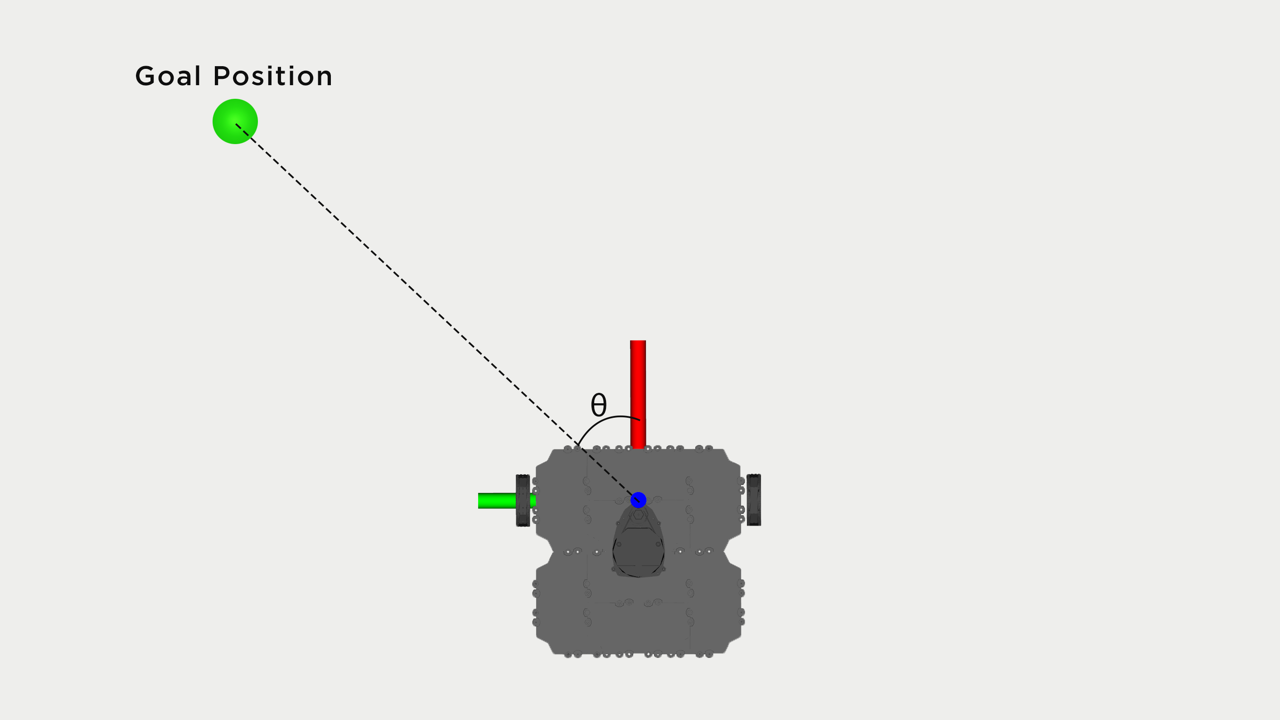
Turtlebot 3 Angle heading

Angular Velocity Calculation:

HeadingAngleToGoal = \arctan { \frac {GoalPositionY { \atop robot }} {GoalPositionX { \atop robot }} }
AngularVelocity = HeadingAngleToGoal * k_0

Linear Velocity Calculation:

DistanceToGoal = \sqrt{\smash[b]{({GoalPositionY_{robot}})^2 + ({GoalPositionX_{robot}})^2 }}
LinearVelocity = f(DistanceToGoal) = \begin{cases} {DistanceToGoal * k_1} &\text{if } | {DistanceToGoal * k_1}|< MaxVelocity \\ MaxVelocity &\text{if } | {DistanceToGoal * k_1}| >=MaxVelocity \\ { } \end{cases}
  • The robot is not moving until the heading of the robot is close enough towards the goal position:
LinearVelocity = f(HeadingAngleToGoal) = \begin{cases} {LinearVelocity } &\text{if } | {HeadingAngleToGoal}|< AngleLimit \\ {0} &\text{if } | {HeadingAngleToGoal}| >=AngleLimit \\ { } \end{cases}

Behavior 2 (Follow Obstacle Boundary)

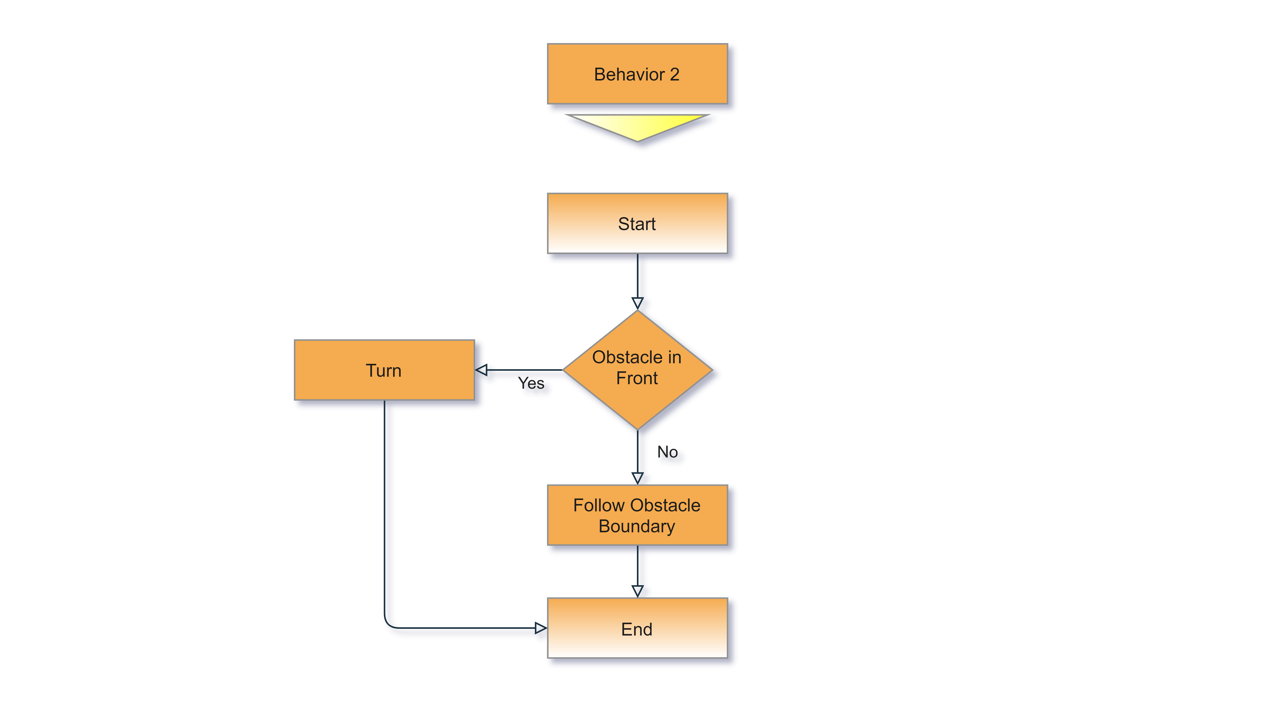
Bug0 Algorithm Behavior 2

  • Following Obstacle Boundary:

Angular Velocity Calculation:

AngularVelocity = (FrontLeft -BackLeft) * k_2
DistanceStabilizer = (FollowDistanceConstant - FrontLeft ) * k_3
AngularVelocity = (AngularVelocity + DistanceStabilizer )
AngularVelocity = \begin{cases} {AngularVelocity } &\text{if } | {AngularVelocity}|< MaxAngularVelocity \\ MaxAngularVelocity &\text{if } | {AngularVelocity}| >=MaxAngularVelocity \\ { } \end{cases}

Linear Velocity Calculation: The robot's linear velocity is proportional to the robot's parallelism to the obstacle.

AngleError = |(FrontLeft - BackLeft)| * k_4
LinearVelocity = \begin{cases} { MaxLinearVelocity - AngleError } &\text{if } {AngleError} < {MinLinearVelocity} \\ MinLinearVelocity &\text{if } {AngleError} >= {MinLinearVelocity} \\ { } \end{cases}

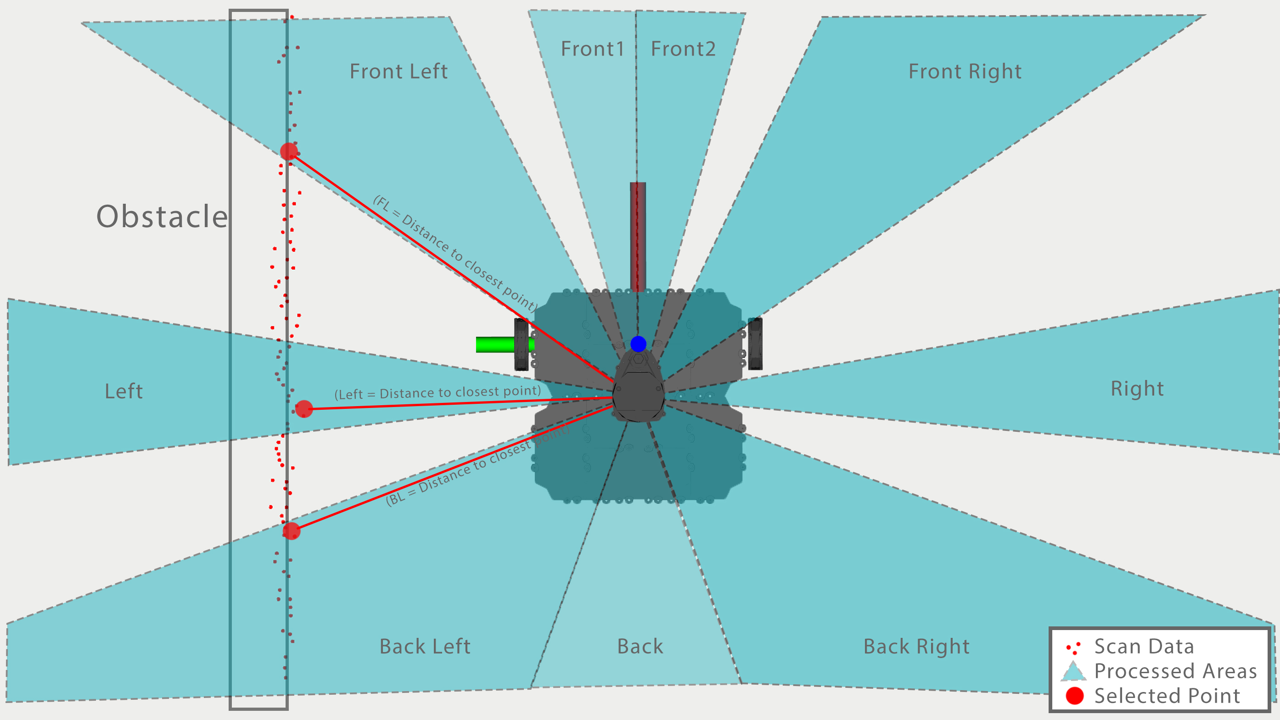
Analysis of Lidar Sensor Data

TB3 Behavior 2 Lidar Sensor Interpretation.jpg




Related Posts

Check out my all posts

Comments




Ryan

4/1/2024
Ryan

could you please, send me the project source code for this "https://www.theconstruct.ai/exploring-ros-2-wheeled-robot-8-bug-0/ " . I would much appreciate it.




1/10/2021
utku olcar
ActionLib, Bug0, Gazebo, LazerScan, Lidar, linux, Marker, Mobile Robotics, Odometry, Python, ROS, rViz, TF, Ubuntu Embedded System Programming, Robotic Calculations, Robotic Programming
1 Comments


© Copyright 2019. All Rights are Reserved.